题目
描述
桌面上放了N个平行于坐标轴的矩形,这N个矩形可能有互相覆盖的部分,求它们组成的图形的面积。
格式
输入格式
输入第一行为一个数N(1≤N≤100),表示矩形的数量。下面N行,每行四个整数,分别表示每个矩形的左下角和右上角的坐标,坐标范围为–10^8到10^8之间的整数。
输出格式
输出只有一行,一个整数,表示图形的面积。
样例1
样例输入1
1 | 3 |
样例输出1
1 | 10 |
题解
这里有篇很好的文章,对于深入理解有帮助
对于这道题目,第一想法就是用bool数组标记,最后统和,但是奈何数据范围不允许。
可以用扫描线+线段树维护,但是总觉得有点大动干戈。
而“离散化”这一奇妙的思想能帮我们优雅地解决这道题(然而样例不能很好体现)
我们首先来看看样例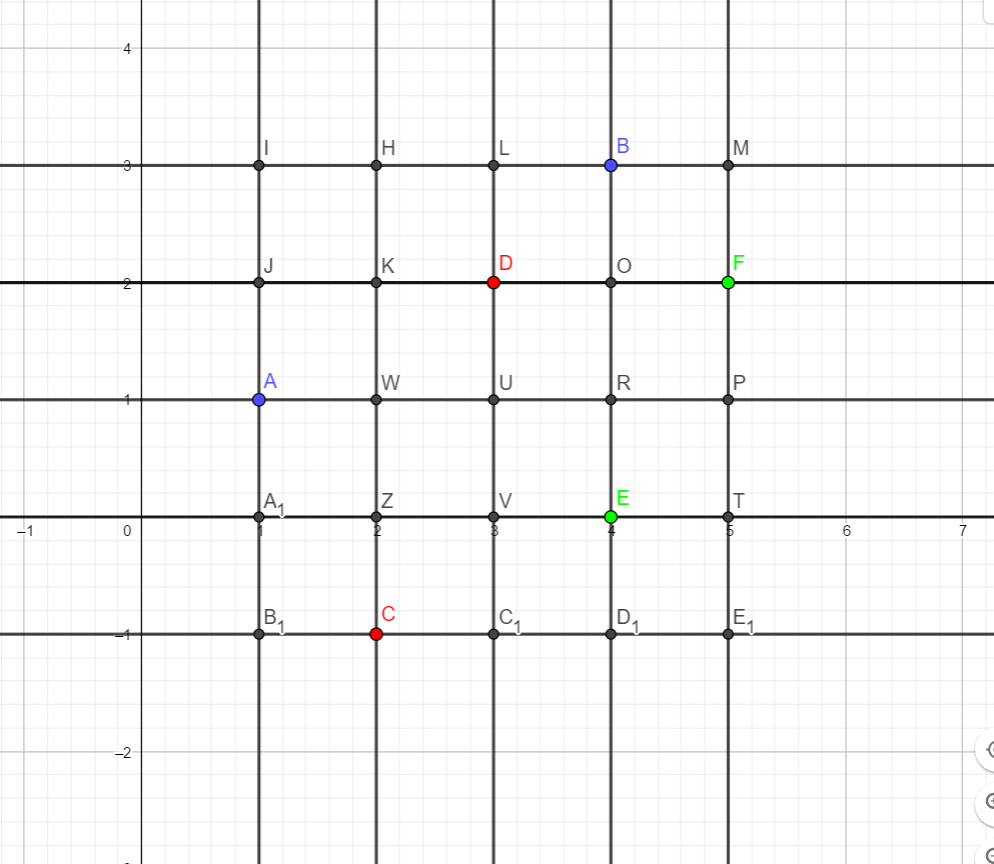
其中一样的颜色的点为一对输入(一个矩形),我们取出它们的横纵坐标,去重,排序,然后再去枚举,就得到了那些黑色的点。(有些和有颜色的点重复了)
其实到了这一步我们已经离散化了(还没明白?别急,先往下看)
于是我们枚举每一个黑色的点,让它和它右上方的黑点构成一个矩形,如果这个矩形在任意输入矩形内部,则对答案有贡献
这样子我们就做到了不重不漏(黑点枚举出来的矩形不重复,并且黑点构成的全部矩形肯定把输入矩形囊括在内)
到这里貌似就结束了,但是这种方法看上去还是在数格子?
让我们把输入改成1
2
3
43
1 1 4 4
2 -1 3 3
4 0 5 3
再看看图像
我们的枚举量并没有随着坐标范围变大而变大,并且还是做到了不重不漏,其原因就是我们在枚举黑点的时候,本来是2的距离,转化成了该点与上个点相差2,而空间上这两个点还是相邻的,这就是离散化。
上面已经解释得很清楚了,代码就不写注释了。
代码
1 |
|